It’s a Funny Old (Game of) Life. But Would You Play a Cellular Automaton Version?
Conway’s Game of Life is a form of artificial life called a cellular automaton. Although the rules are simple, the results can be amazing.
July 1, 2021

Did you ever see The Mummy movie from 1999 staring Brendan Frazer? (I also loved Brendan in his role in George of the Jungle from 1997.) There’s a part in the movie when thousands of scarabs -- which aredepicted as being deadly, ancient beetles that eat internal and external organs -- boil up out of the ground and start devouring everyone in sight. (On the off chance you were wondering, the five external organs are considered the eyes, ears, nose, tongue, and skin.)
These creatures are animated, but did you ever think about how this animation was achieved? It would take a mind-boggling amount of time and effort to individually direct the actions of each of these insects. The trick is first to define how an individual scarab might move and set up a simple set of rules that determine how a scarab might react to any objects and other scarabs in the vicinity. After this, all you have to do is define the paths of a handful of “leader scarabs,” and the rest will follow along.
The first example I saw of this sort of thing was an artificial life simulation program called Boids, developed by computer graphics guru Craig Reynolds in 1986. The “Boid” moniker originated as a shortened version of “bird-oid object” (i.e., “bird-like object”). By some strange quirk of fate, “boid” is also the way folks pronounce “bird” in the metropolis of New York.
A good summary of this concept is provided by Wikipedia, which tells us that: “As with most artificial life simulations, Boids is an example of emergent behavior; that is, the complexity of Boids arises from the interaction of individual agents (the boids, in this case) adhering to a set of simple rules. The rules applied in the simplest Boids worlds are as follows: separation (steer to avoid crowding local flockmates), alignment (steer towards the average heading of local flockmates), and cohesion (steer to move towards the average position (center of mass) of local flockmates). More complex rules can be added, such as obstacle avoidance and goal-seeking.”
Just to give you an idea of what I’m talking about, take a look at this video from 2007 showing a flock of boids following a target (a green ball) and avoiding a fixed object (a red sphere). Of course, similar behaviors can be applied to sholes of fish, as seen in this simulation, or scarabs in horror movies.
Another form of artificial life is that of cellular automaton (plural cellular automata, abbreviation CA). A CA involves a “universe” formed from a grid of cells, each of which can be in one of a finite number of states. The state of each cell is affected by the conditions of other cells in its local neighborhood. At the beginning of the simulation, an initial “seed” state is applied to the cells, after which a small number of rules are employed to proceed from one generation to the next.
The CA concept was initially discovered in the 1940s by Stanislaw Ulam and John von Neumann. At the same time, they were contemporaries at Los Alamos National Laboratory. Still, things didn’t take off until 1970 when the British mathematician John Horton Conway invented his CA called the Game of Life (GOL).
Conway was something of a “character” described as being like “Archimedes, Mick Jagger, Salvador Dali, and Richard Feynman all rolled into one.” In its original two-dimensional (2D) incarnation, the universe in which the GOL takes place is an infinite grid of square cells (more recently, some people have experimented with three-dimensional (3D) universes formed from an endless array of cubic cells).
Each cell in the GOL can be in one of two possible states: “alive” or “dead.” Also, each cell interacts with its eight “neighbors,” which are those cells that are horizontally, vertically, or diagonally adjacent. Thus, we start by seeding the universe with some pattern, which might involve some specific combination(s) of cells, or it could be randomly generated. We then let the simulation evolve from one generation to the next using the following set of rules:
Any live cell with fewer than two live neighbors dies, as if by underpopulation.
Any live cell with two or three live neighbors lives on to the next generation.
Any live cell with more than three live neighbors dies, as if by overpopulation.
Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
Births and deaths occur simultaneously, and each new generation is a pure function of the preceding generation. Thus, although these rules may appear simple when you read them, it can take some mental gymnastics to apply them. Consider the following illustration, for example:
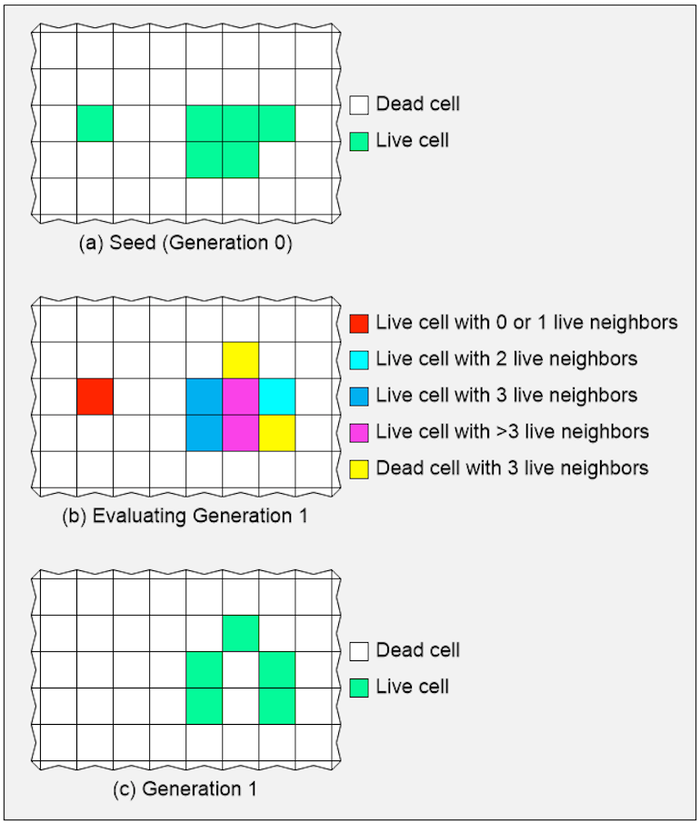
We start with our seed generation, which we can think of as “Generation 0.” We then consider each cell in the context of its neighbors. For each cell, there are two choices. If a cell is currently alive, it will either remain alive or die in the next generation. Similarly, if a cell is now dead, it will either stay dead or spring to life in the next generation.
You must admit that working out what will happen is not too easy if you’re doing it by hand. But, of course, it’s easy peasy lemon squeezy if you have a computer to do it for you. The amazing thing to me is that Conway didn’t have access to the computer when he invented his GOL. Instead, he and his colleagues spent countless hours playing with pebbles on a GO board to determine the optimum set of rules they ended up with.
The exciting thing is that, although the GOL rules themselves are straightforward, the resulting behavior can be highly complex. For example, some patterns are known as “Still Lifes” because they remain static from one generation to the next unless they are disturbed by encroaching cells. The next level up is “Oscillators,” which return to their initial state after a finite number of generations. Next up, we have “Spaceships,” which translate themselves (move) across the grid (the simplest of these is the “Gosper glider,” which was discovered by Bill Gosper in 1970). And we also have “guns,” which are patterns that have a central part that repeats periodically, like an oscillator, and that also sometimes emit spaceships. All I can say is that a full-up GOL simulation is something to behold (search for “Game of Life” on YouTube to see some notable examples).
The reason I’m waffling on about all of this here is because I decided to implement a GOL of my very own. As you may recall from earlier columns (see Ping Pong Ball Array Shines and Easily Add Motion and Orientation Sensing to Improve Your Projects), I created a 12x12 ping pong ball array, where each ball is equipped with a tricolor LED. Since I already had this array at my disposal, I decided to use it as the display mechanism for a simple GOL.
Of course, one problem is that the GOL universe is supposed to be infinite, so a 12x12 array of sells falls a little short. The way I got around this was to make my array universe “curved.” We can imagine our universe as being rolled into a vertical cylinder such that the right-hand side wraps around and meets the left-hand side, so a spaceship “exiting stage right” will “reappear stage left.” Similarly, and simultaneously, we can imagine our universe as being rolled into a horizontal cylinder such that the top side wraps around and meets the bottom side, so anything “falling off the bottom” will reappear at the top.
The best way to visualize this is to watch it in action. As depicted in this video, we start by loading the array with a random seed, run the simulation until all the cells are dead, and then start all over again. Unfortunately, the first two random patterns fade away rather quickly. However, the third random seed proves to be much more interesting.
The funny thing is that when I originally built my 12x12 array, I had no idea as to all the things I would end up doing with it. Now, new ideas pop into my mind almost every day. For example, I think about building a bigger (wall-sized) array -- I can only imagine what a GOL would look like on that. How about you? Do you have any thoughts you’d care to share on any of this?
Clive “Max” Maxfield received his B.Sc. in Control Engineering from Sheffield Hallam University in England in 1980. He began his career as a designer of central processing units (CPUs) for mainframe computers. Over the years, Max has designed all sorts of interesting “stuff” from silicon chips to circuit boards and brainwave amplifiers to Steampunk Prognostication Engines (don’t ask). He has also been at the forefront of electronic design automation (EDA) for more than 30 years. Already a noted author of over a half-dozen books, Max is always thinking of his next project. He would particularly like to write for teens, introducing them to engineering and computers in a fun and exciting way. For this is what sets “Max” Maxfield apart: It is not just what he knows, but how he relates it to the learner.
About the Author(s)
You May Also Like




.jpg?width=300&auto=webp&quality=80&disable=upscale)
