How Are Resistor Values Like French Army Hot Air Balloons From the 1800s?
What is the strange relationship between resistor values and the hot air balloons fielded by the French Army in the late 1800s?
May 28, 2021

If you’ve been involved in electronics for any length of time, you probably don’t give much thought to the various values associated with resistors. By comparison, newcomers to the field are often puzzled as to why we have resistor values like 12 kΩ, 15 kΩ, 18 kΩ, 22 kΩ, 27 kΩ, 33 kΩ, 39 kΩ, and so forth. So why not keep things simple and just have ten kΩ, 20 kΩ, 30 kΩ, 40 kΩ, etc.? The reasoning behind this is actually rather interesting, but first, let’s consider the basics.
When we design an electronic circuit, after performing appropriate calculations, we may decide that -- in an ideal world -- we would like to use a resistor with a value of precisely xxx Ω (where the Greek letter Omega is used to represent resistance in ohms).
One approach would be to handcraft individual resistors with specific values as and when required, but this would be expensive and time-intensive. The alternative is to have access to affordable, pre-constructed, off-the-shelf components. The problem here is that manufacturers couldn’t create and supply every conceivable value and -- even if they could -- the users of the resistors couldn’t afford to purchase all of these parts and wouldn’t have sufficient space to store them.
The solution arrived at by the industry was to adopt a set of standard resistor values. This comes with the added advantage of allowing users to second source their resistors from multiple manufacturers. But now we have the question as to which resistor values should be included in the set.
Now, hold onto your hats because we are about to take a journey back in time. In 1877, a French military engineer called Charles Renard was presented with a poser. At that time, the French army had a bunch (not the technical term) of hot-air balloons that they used to spy out enemy positions and drop bombs on anyone who criticized French cuisine. Before Renard appeared on the scene to keep their balloons in the air, the army was obliged to maintain 425 different ropes, which was a logistical nightmare. Renard was tasked with somehow reducing this number to a more manageable quantity.
People like Renard amaze me because I could never see myself conceiving the things they do. In this case, Renard realized that if a product is to be manufactured in a range of sizes, then one way to minimize the number of different sizes that need to be manufactured or kept in stock is to choose them such that they are roughly equally spaced on a logarithmic scale.
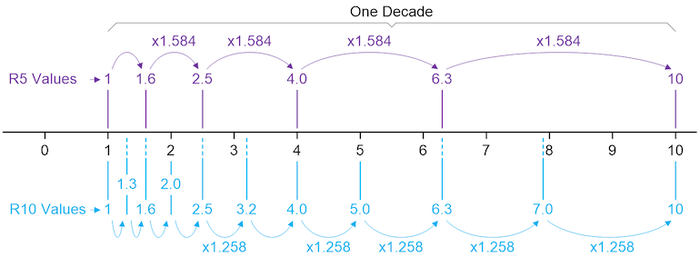
In Renard’s system, the interval from 1 to 10 was divided into 5, 10, 20, or 40 steps, which we now refer to as the R5, R10, R20, and R40 scales. Let’s start with the R5 scale, which can be represented mathematically as follows:
10(0/5) = 1
10(1/5) = 1.584... ≈1.6
10(2/5) = 2.511... ≈2.5
10(3/5) = 3.981... ≈4.0
10(4/5) = 6.309... ≈6.3
10(5/5) = 10
Observe that, since this scheme is based on a logarithmic approach, each new number can be generated by multiplying the previous value by 10(1/5) = 1.584 and rounding as required.
One great thing about the logarithmic approach is that we can repeat it decade by decade. The example above was for the decade 1 to 10, but the same thing applies for decades 10 to 100, 100 to 1,000, 1,000 to 10,000, and so forth. Another cool characteristic of this logarithmic approach is that if we decide to move to a higher resolution scale, then the values from the lower resolution scale also appear in the more comprehensive scale. Take the R10 scale, for example:
10(0/10) = 1 (Same as for the R5 Scale)
10(1/10) = 1.258... ≈1.3
10(2/10) = 1.584... ≈1.6 (Same as for the R5 Scale)
10(3/10) = 1.995... ≈2.0
10(4/10) = 2.511... ≈2.5 (Same as for the R5 Scale)
10(5/10) = 3.162... ≈3.2
10(6/10) = 3.981... ≈4.0 (Same as for the R5 Scale)
10(7/10) = 5.011... ≈5.0
10(8/10) = 6.309... ≈6.3 (Same as for the R5 Scale)
10(9/10) = 7.943... ≈7.9
10(10/10) = 10 (Same as for the R5 Scale)
In this case, each new number can be generated by multiplying the previous value by 10(1/10) = 1.258 and rounding as required. The best way to wrap one’s head about this if you are a beginner is by means of a graphical representation, as shown below.
As we mentioned earlier, before Renard appeared on the scene, the French army was obliged to maintain 425 different sizes of ropes in order to keep its hot air balloons in the air. After Renard had come up with his preferred values based on logarithmic scales, this number was reduced to just 17, thereby making him the “toast of the town” with regard to the army’s quartermasters. (Sad to relate, Renard was never again to be invited to a soiree hosted by the rope maker’s guild.)
Renard’s R5, R10, R20, and R40 scales were officially adopted as standards by the International Organization for Standardization (ISO) in the early 1950s and are employed by various disciplines. In the case of electronics, for example, they are used for such applications as the current rating of electric fuses and the voltage rating of capacitors (e.g., 100 V, 160 V, 250 V, 400 V, 630 V).
Having said all this, Renard’s scales aren’t used for resistors. In 1952, the IEC (International Electrotechnical Commission) defined a set of standard values for different types of components, including resistors. Collectively referred to as the “E series,” this actually consists of the E3, E6, E12, E24, E48, E96, and E192 series, where the number after the ‘E’ designates the quantity of value “steps” in each series. In the case of the E12 series, for example, this could be represented mathematically as follows:
10(0/12) = 1
10(1/12) ≈ 1.2
10(2/12) ≈ 1.5
10(3/12) ≈ 1.8
10(4/12) ≈ 2.2
10(5/12) ≈ 2.7
10(6/12) ≈ 3.3
10(7/12) ≈ 3.9
10(8/12) ≈ 4.7
10(9/12) ≈ 5.6
10(10/12) ≈ 6.8
10(11/12) ≈ 8.2
10(12/12) = 10
In this case, each new number can be generated by multiplying the previous value by 10(1/12) = 1.2115… ≈1.21. Furthermore, remembering that these values repeat every decade, we can summarize them in a table as shown below.
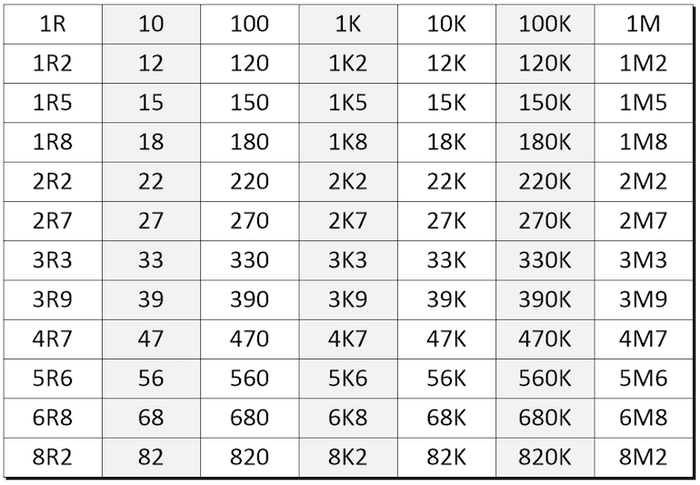
With regard to the values shown like 3R9, 3K9, and 3M9 in the above table, this is just another way of saying 3.9 Ω, 3.9 KΩ, and 3.9 MΩ, respectively. The problem with using decimal points is that they can be easy to miss and/or they can become obscured in printed materials, in which case 3.9 Ω, 3.9 kΩ, and 3.9 MΩ could easily be mistaken for 39 Ω, 39 kΩ, and 39 MΩ, respectively.
In conclusion, and to answer our original question, it now becomes clear why we work with resistor values like 12 kΩ, 15 kΩ, 18 kΩ, 22 kΩ, 27 kΩ, 33 kΩ, 39 kΩ, and so forth. As always, I welcome your comments, questions, and suggestions.
Clive “Max” Maxfield received his B.Sc. in Control Engineering from Sheffield Hallam University in England in 1980. He began his career as a designer of central processing units (CPUs) for mainframe computers. Over the years, Max has designed all sorts of interesting “stuff” from silicon chips to circuit boards and brainwave amplifiers to Steampunk Prognostication Engines (don’t ask). He has also been at the forefront of electronic design automation (EDA) for more than 30 years. Already a noted author of over a half-dozen books, Max is always thinking of his next project. He would particularly like to write for teens, introducing them to engineering and computers in a fun and exciting way. For this is what sets “Max” Maxfield apart: It is not just what he knows, but how he relates it to the learner.
About the Author(s)
You May Also Like