Mechatronify Common Mechanisms

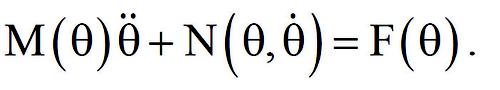
What does it mean to mechatronify a mechanism or machine? In life, how you do something is more important than what you do. Mechatronics is more than just adding a sensor, an actuator, and a computer control system. They must be added in an integrated way from the very start of the design and, just as importantly, using a model-based design process that takes advantage of analysis techniques and simulation software and leads to optimum designs without trial and error.

Combining old inventions with new technology fosters innovative ideas, but it is the process that transforms these ideas into reality. Let's use as an example a mechanism that was developed by Leonardo da Vinci more than 500 years ago and now is found in engines, automation applications, and miniature devices around the world -- the slider crank. Let's illustrate how to mechatronify this Renaissance mechanism.

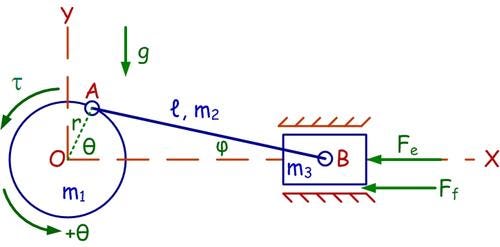
This is a diagram of a slider-crank mechanism, consisting of a flywheel crank, a connecting rod, and a slider, all of which are assumed to be rigid. The external forces/torques acting are the servomotor torque τ, the slider friction force F_f, and the external force F_e. It is a special case of the four-bar linkage where one crank is infinite in length, such that its end point (point B) has rectilinear motion. It is a one-degree-of-freedom system, because only one coordinate is needed to describe its motion completely. The constraint equation relating angles Θ and φ is

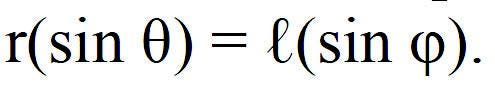
Kinematic analysis (i.e., the geometry of motion) can be carried out graphically, yielding great insight. However, a mathematical solution is much more effective for mechatronic system design and optimization. Positions, velocities, and accelerations of key points are obtained, as well as the angular velocities and angular accelerations of the rigid bodies.

Kinetic analysis can be accomplished by drawing free-body diagrams showing gravitational forces, contact forces/torques, and the inertia forces/torques and then summing forces/moments as needed. This is known as the D'Alembert approach to applying Newton's laws, and forces/torques at all joints can be determined.  The system equation of motion is directly obtained by the application of Lagrange's Equation,

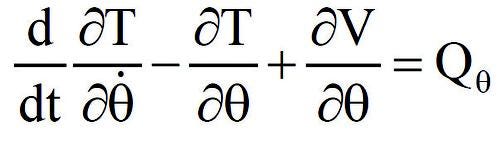
using the generalized coordinate θ where V is the system potential energy, T is the system kinetic energy, and Q_θ is the generalized torque due to forces/torques that do work. The resulting equation has the form

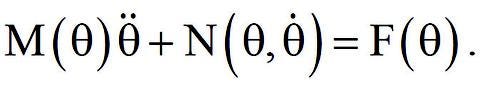
Once the kinematic and kinetic analyses are completed, the desired end-point trajectory must be defined. Then, through inverse kinematics, which includes here the crank and connecting rod lengths, the necessary motion profile for the actuator is computed.

This is accomplished by trajectory planning. This profile needs to be defined in a way to avoid or reduce the mechanical vibration and stress on components and actuators, as well as to reduce overshoot response and excessive position error during motion. This is accomplished by electronic cams. The inverse kinetic analysis, which includes masses, center-of-mass locations, and mass moments of inertia, is used to generate the required actuator torque/force for the motion profile. This produces a speed/torque-force diagram on which to base actuator selection. The chosen actuator becomes part of the system, and a control system with feedback, feed forward, and disturbance observer is designed with the updated system. This results in a new speed/torque-force profile. The entire system should now be simulated, with the addition of any parasitic effects, for design validation.

Through this process, innovative ideas become a reality. Sweating the details with a combination of knowledge (old and new), process, and determination will make innovation happen.

Vist the Mechatronics Zone on DesignNews.com for all the latest Mechatronics news.