Wilbur Wright Understood It

Wilbur Wright owned a bicycle shop with his brother Orville. Wilbur's understanding of complex, dynamic problems contributed to the Wright brothers' successful first airplane flight.

Wilbur understood, for example, that to turn a bicycle to the left, one first turns the handlebars a little to the right, and then, as the bicycle inclines to the left, one turns the handlebars to the left. He understood counter-steering.

In mathematical language, the transfer function between the steer torque applied to the handlebars and the straight-line-path deviation has a right-half-plane zero which imposes a limit on maneuverability. The path deviation has an inverse-response behavior, i.e., in response to a positive step-torque input applied to the handlebars, the path deviation is initially positive then becomes negative. This has contributed to numerous motorcycle accidents, but counter-steering could prevent these accidents.

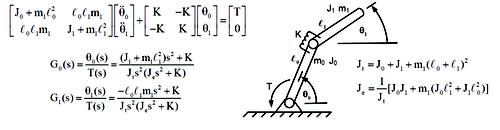
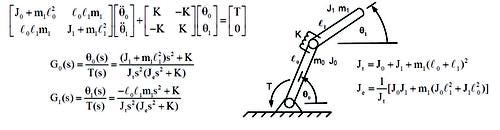
The bicycle is a very complicated dynamic system. Let's use a simpler system to better understand the physical significance of the poles and zeros of a transfer function. Consider the system shown consisting of two rigid links and a torsional spring. Assume small displacements. The equations of motion are shown in matrix form, along with two transfer functions: G0(s) and G1(s).

A pole of a transfer function is a value of s that makes the denominator equal to zero, while a zero of a transfer function is a value of s that makes the numerator equal to zero. Systems that have no poles or zeros in the right half of the complex plane (RHP) are called minimum-phase systems, as either of the two components of the frequency response, gain and phase, contains all the frequency response information that exists. This is called Bode's Gain-Phase Relationship. Systems that have poles in the RHP are unstable. A nonminimum-phase stable system is one that has a zero in the RHP. Examples of physical phenomena that give rise to nonminimum-phase stable behavior include control of the level of a volume of boiling water and hydroelectric power generation.

The denominators of both transfer functions are identical. The double pole at the origin represents the rigid-body motion of the system. The complex-conjugate pole pair represents the natural frequency associated with the energy storage characteristics, kinetic and potential energy, of the physical system. They are independent of the locations of the sensor (0 or 1) and actuator (T). At a frequency of the complex pole, energy can freely transfer back and forth between the kinetic and potential energy, and the system behaves as an energy reservoir.

The numerators of the two systems are quite different. The complex zero represents the natural frequency associated with the energy storage characteristic of a sub-portion of the system defined by artificial constraints imposed by the sensor and actuator, i.e., the resonant frequency of the second link when the first link is fixed. It is lower than the natural frequency of the system. It corresponds to the frequency where the system behaves as an energy sink, such that energy being applied by the input is completely trapped in the energy storage elements of a sub-portion of the original system such that no output can ever be detected at the point of measurement. The zero in the RHP is called a nonminimum phase zero and gives rise to the same characteristic initial inverse response Wilbur Wright observed in the bicycle.

The location of the poles and zeros of a transfer function are the result of design decisions and can make control easy or hard.

Vist the Mechatronics Zone on DesignNews.com for all the latest Mechatronics news.