Nothing Is Instantaneous

We experience it every morning as we struggle to find the right water temperature in the shower. Time delays are everywhere. They arise in engineering, biology, physics, economics, and the environment. As engineering systems become more complex, multiple sensors, actuators, and controllers introduce multiple delays, particularly in interconnected and distributed systems. In a dynamical system, changes cannot be effected instantaneously, and so an otherwise correct control decision applied at the wrong time could result in catastrophe.

From our first exposure to feedback control systems, we are taught always to conserve phase. What is the relationship between time delay and phase? How are they related to the stability of a feedback control system? Does time delay always degrade the performance of a feedback control system?

Time delays arise in control systems from delays in the process itself (represented by time constants τ and natural frequencies ω_n in transfer functions), from delays in the processing of sensed signals, and from delays in the implementation of a digital control system as a result of sample-and-hold, calculation, and velocity estimation, where the total time delay can be between one and two times the sample period.

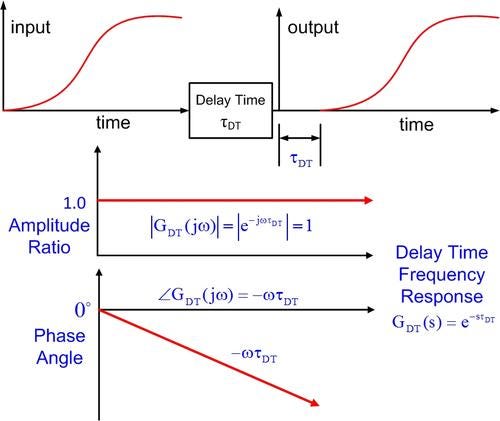
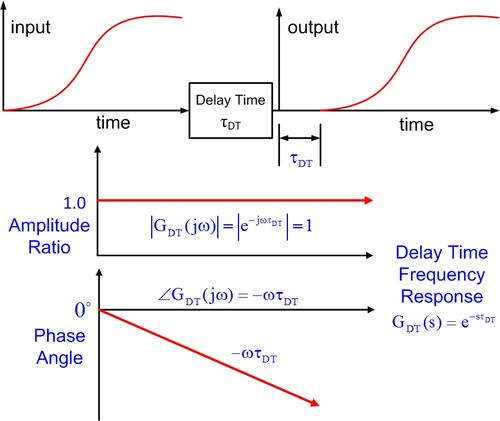
The input-output time delay shifts the signal in time and is shown in the figure above. The frequency response of a time delay is exact with a magnitude of one and a phase angle that decreases linearly with frequency. A bigger time delay corresponds to a faster increase of phase lag with frequency.

Why does time delay (and, correspondingly, phase lag) almost always cause a system to go unstable? Physically, an imbalance between the strength of the corrective action and the system dynamic lags results in the corrective action being applied in the wrong direction. Mathematically, when the denominator of the closed-loop transfer function equals zero, the system goes unstable. Since this denominator is equal to 1 + the open-loop transfer function, when the open-loop transfer function equals -1 (i.e., magnitude = 1, and phase angle = -180 degrees), the closed-loop system is marginally stable.

If a system is stable, how close is it to becoming unstable? Because of model uncertainties, it is not sufficient for a system merely to be stable; it must have adequate stability margins.

Stable systems with low stability margins work only on paper. The way uncertainty has been quantified in classical control is to assume that either gain changes or phase changes occur. The tolerances of gain or phase uncertainty are the gain margin and the phase margin. A paradox is that the presence of delays may be either beneficial or detrimental to the operation of a dynamical system. Judicious introduction of a delay may stabilize an otherwise unstable system (e.g., a wait-and-act control strategy) or improve steady-state tracking error.

The impact of delays continues to grow in many fields, including the control of distributed systems such as energy and computing grids.

Vist the Mechatronics Zone on DesignNews.com for all the latest Mechatronics news.