Measure Frequency Response on Fully Differential Amplifiers Using Complex Algebra

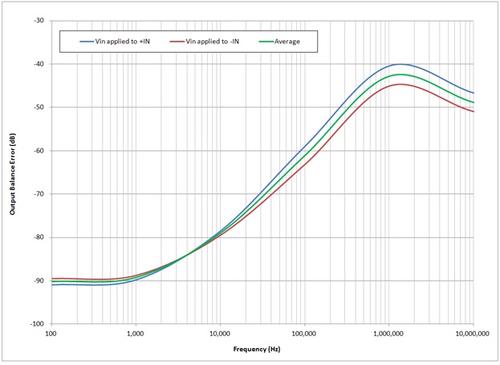
Evaluating the error frequency responses of a fully differential amplifier can be difficult and time consuming if standard measurement techniques are used. This is because the task requires measuring small differential and common-mode error signals. For example, evaluating the amplifier's power supply rejection (PSR) and common-mode rejection (CMR) over frequency requires measuring differential error voltages, while evaluating the amplifier's output balance over frequency requires measuring common-mode error voltages. At low frequencies, these error voltages can be in the order of microvolts.

Traditional methods of measuring the different frequency responses of a fully differential amplifier require either expensive lab equipment (like a differential network analyzer) or specialty interface circuitry to cope with the amplifier's differential output. The complex algebra method uses superposition to reconstruct the amplifier's differential and common-mode output voltages from single-ended output voltage measurements. Since the measurements are single-ended, a single-ended network analyzer can be used without an interface circuit. To perform these measurements, a vector analyzer is preferred since it can output the measured waveforms in complex number form, a data representation that can be easily manipulated during the reconstruction process.

Measurement steps:

Measurement Example 1
In our example, we'll measure the PSR+ of an amplifier, the AD8476, using a Rohde & Schwartz network analyzer. Characterizing an amplifier's PSR+ over frequency is challenging because the input excitation must be injected to the amplifier's power bus. If the amplifier is fully differential, the challenge becomes even greater because you must measure the output voltage's differential-mode component while rejecting the common-mode component. Luckily, the measurement can be simplified using the complex algebra method.