FIR Filter Coefficients
September 6, 2013
The first part of this series described how data flows through processing steps that create a moving average of stock prices over 65 days. Finite-impulse-response (FIR) filters use the same data-flow topology, but with coefficients that have different values. In both cases, software performs a convolution between the coefficients and incoming data to indicate how well the coefficients overlap with the data in the time domain.
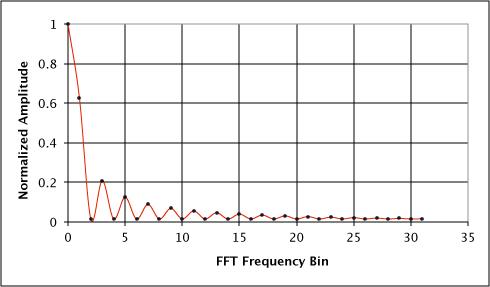
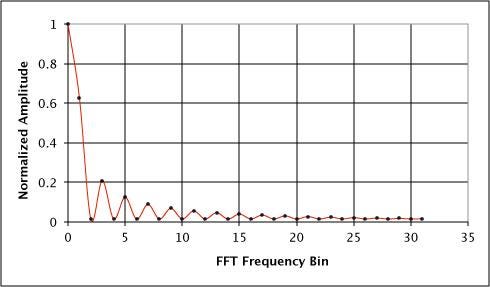
To show how this process works, I'll move to the frequency domain. The diagram below shows the discrete Fourier transform (DFT) of the 65 equal coefficients (0.015625) used to produce the daily price average. Here you can see the characteristics of a low-frequency filter. A DFT output from a set of FIR filter coefficients produces a similar frequency versus amplitude graph of that filter's output.
Suppose you wanted to created a FIR filter with your own requirements. How would you find the necessary coefficients, and how many of them would you need? You can draw on several mathematical techniques -- windowing, frequency-sampling, Parks-McClellan, and least-squares, for example. But most engineers use software expressly created to help with FIR filter designs. Microchip Technology's filter design software creates filters for dsPIC microcontrollers. The PSoC Creator from Cypress Semiconductor produces coefficients for low-pass and band-pass FIR filter blocks in the company's programmable system on a chip (PSoC) devices.
For these columns, I used the Professional ScopeFIR software from Iowegian International to calculate coefficients for low-pass filters within a narrow range of sampling frequencies, cutoff frequencies, attenuations, and pass-band ripples. The software estimates the number of coefficients (also called taps) and calculates coefficient values. A pass/fail notation lets me know whenever I needed to increase the number of taps to meet a set of filter requirements.
One low-pass filter required only seven coefficients. Another needed 44. That number arose from a filter with a 1,500Hz pass-band cutoff frequency and a 2,000Hz stop-band cutoff frequency at -80dB. That's a sharp filter that's difficult to create with op-amps and passive components. The coefficients appear in a list with 18-digit resolution. ScopeFIR windows display each filter's impulse response and a plot of frequency versus attenuation.
In the next column in this series, I will create an FIR filter in an ARM Cortex-M3 microcontroller and explain the results.
Thanks go to Grant Griffin at Iowegian International for use of the Professional ScopeFIR software. Iowegian has software for IIR filter design and for Fourier transforms.
For more information:
Cypress Semiconductor filter block information
PSoC information
Microchip Technology filter design software
Related posts:
About the Author(s)
You May Also Like